How To Draw A Bayesian Network

A Gentle Introduction to Bayesian Conventionalities Networks

Probabilistic models can ascertain relationships between variables and be used to calculate probabilities.

For example, fully conditional models may require an enormous corporeality of data to cover all possible cases, and probabilities may be intractable to summate in do. Simplifying assumptions such as the provisional independence of all random variables can exist effective, such as in the instance of Naive Bayes, although it is a drastically simplifying step.

An culling is to develop a model that preserves known conditional dependence betwixt random variables and provisional independence in all other cases. Bayesian networks are a probabilistic graphical model that explicitly capture the known provisional dependence with directed edges in a graph model. All missing connections define the conditional independencies in the model.

Equally such Bayesian Networks provide a useful tool to visualize the probabilistic model for a domain, review all of the relationships between the random variables, and reason almost causal probabilities for scenarios given bachelor evidence.

In this post, you volition discover a gentle introduction to Bayesian Networks.

Afterward reading this postal service, y'all will know:

• Bayesian networks are a blazon of probabilistic graphical model comprised of nodes and directed edges.
• Bayesian network models capture both conditionally dependent and conditionally independent relationships between random variables.
• Models can be prepared past experts or learned from information, and so used for inference to judge the probabilities for causal or subsequent events.

Kicking-start your projection with my new volume Probability for Machine Learning, including step-by-footstep tutorials and the Python source code files for all examples.

Let'southward go started.

A Gentle Introduction to Bayesian Belief Networks
Photo by Armin S Kowalski, some rights reserved.

Overview

This tutorial is divided into five parts; they are:

1. Challenge of Probabilistic Modeling
2. Bayesian Conventionalities Network every bit a Probabilistic Model
3. How to Develop and Use a Bayesian Network
4. Example of a Bayesian Network
5. Bayesian Networks in Python

Claiming of Probabilistic Modeling

Probabilistic models can be challenging to design and use.

Most often, the trouble is the lack of data about the domain required to fully specify the conditional dependence between random variables. If available, calculating the full conditional probability for an event can be impractical.

A common approach to addressing this challenge is to add some simplifying assumptions, such as assuming that all random variables in the model are conditionally contained. This is a drastic assumption, although information technology proves useful in exercise, providing the basis for the Naive Bayes classification algorithm.

An alternative arroyo is to develop a probabilistic model of a problem with some provisional independence assumptions. This provides an intermediate arroyo between a fully conditional model and a fully conditionally contained model.

Bayesian conventionalities networks are ane example of a probabilistic model where some variables are conditionally independent.

Thus, Bayesian belief networks provide an intermediate approach that is less constraining than the global assumption of conditional independence fabricated past the naive Bayes classifier, but more tractable than avoiding conditional independence assumptions birthday.

— Folio 184, Motorcar Learning, 1997.

Want to Learn Probability for Machine Learning

Take my gratuitous 7-day email crash course now (with sample code).

Click to sign-upwardly and as well become a complimentary PDF Ebook version of the course.

Bayesian Belief Network as a Probabilistic Model

A Bayesian belief network is a blazon of probabilistic graphical model.

Probabilistic Graphical Models

A probabilistic graphical model (PGM), or simply "graphical model" for short, is a way of representing a probabilistic model with a graph construction.

The nodes in the graph represent random variables and the edges that connect the nodes represent the relationships between the random variables.

A graph comprises nodes (also called vertices) connected past links (besides known every bit edges or arcs). In a probabilistic graphical model, each node represents a random variable (or group of random variables), and the links express probabilistic relationships betwixt these variables.

— Page 360, Pattern Recognition and Machine Learning, 2006.

• Nodes: Random variables in a graphical model.
• Edges: Relationships between random variables in a graphical model.

There are many different types of graphical models, although the two well-nigh normally described are the Hidden Markov Model and the Bayesian Network.

The Hidden Markov Model (HMM) is a graphical model where the edges of the graph are undirected, meaning the graph contains cycles. Bayesian Networks are more restrictive, where the edges of the graph are directed, meaning they can but be navigated in one direction. This means that cycles are not possible, and the structure tin be more mostly referred to as a directed acyclic graph (DAG).

Directed graphs are useful for expressing causal relationships between random variables, whereas undirected graphs are better suited to expressing soft constraints between random variables.

— Page 360, Pattern Recognition and Machine Learning, 2006.

Bayesian Belief Networks

A Bayesian Belief Network, or just "Bayesian Network," provides a simple style of applying Bayes Theorem to complex problems.

The networks are not exactly Bayesian by definition, although given that both the probability distributions for the random variables (nodes) and the relationships between the random variables (edges) are specified subjectively, the model tin can be idea to capture the "belief" about a complex domain.

Bayesian probability is the study of subjective probabilities or belief in an outcome, compared to the frequentist approach where probabilities are based purely on the past occurrence of the event.

A Bayesian Network captures the joint probabilities of the events represented past the model.

A Bayesian belief network describes the joint probability distribution for a ready of variables.

— Page 185, Auto Learning, 1997.

Central to the Bayesian network is the notion of conditional independence.

Independence refers to a random variable that is unaffected by all other variables. A dependent variable is a random variable whose probability is provisional on 1 or more other random variables.

Provisional independence describes the human relationship among multiple random variables, where a given variable may exist conditionally independent of one or more than other random variables. This does non mean that the variable is independent per se; instead, it is a clear definition that the variable is contained of specific other known random variables.

A probabilistic graphical model, such as a Bayesian Network, provides a mode of defining a probabilistic model for a complex problem past stating all of the provisional independence assumptions for the known variables, whilst allowing the presence of unknown (latent) variables.

Every bit such, both the presence and the absence of edges in the graphical model are of import in the interpretation of the model.

A graphical model (GM) is a way to represent a articulation distribution by making [Conditional Independence] CI assumptions. In particular, the nodes in the graph represent random variables, and the (lack of) edges represent CI assumptions. (A better name for these models would in fact be "independence diagrams" …

— Page 308, Machine Learning: A Probabilistic Perspective, 2012.

Bayesian networks provide useful benefits equally a probabilistic model.

For example:

• Visualization. The model provides a direct way to visualize the structure of the model and motivate the design of new models.
• Relationships. Provides insights into the presence and absenteeism of the relationships betwixt random variables.
• Computations. Provides a mode to construction circuitous probability calculations.

How to Develop and Use a Bayesian Network

Designing a Bayesian Network requires defining at least three things:

• Random Variables. What are the random variables in the problem?
• Conditional Relationships. What are the conditional relationships betwixt the variables?
• Probability Distributions. What are the probability distributions for each variable?

It may be possible for an expert in the problem domain to specify some or all of these aspects in the blueprint of the model.

In many cases, the architecture or topology of the graphical model tin can be specified past an expert, but the probability distributions must be estimated from data from the domain.

Both the probability distributions and the graph construction itself tin can be estimated from data, although it can be a challenging process. As such, it is common to use learning algorithms for this purpose; for case, bold a Gaussian distribution for continuous random variables gradient ascent for estimating the distribution parameters.

Once a Bayesian Network has been prepared for a domain, information technology tin exist used for reasoning, east.g. making decisions.

Reasoning is achieved via inference with the model for a given state of affairs. For example, the consequence for some events is known and plugged into the random variables. The model can be used to estimate the probability of causes for the events or possible further outcomes.

Reasoning (inference) is so performed by introducing evidence that sets variables in known states, and afterward computing probabilities of interest, conditioned on this testify.

— Page 13, Bayesian Reasoning and Machine Learning, 2012.

Applied examples of using Bayesian Networks in practice include medicine (symptoms and diseases), bioinformatics (traits and genes), and speech recognition (utterances and time).

Example of a Bayesian Network

We can make Bayesian Networks concrete with a small instance.

Consider a problem with three random variables: A, B, and C. A is dependent upon B, and C is dependent upon B.

We can country the conditional dependencies as follows:

• A is conditionally dependent upon B, eastward.thou. P(A|B)
• C is conditionally dependent upon B, e.g. P(C|B)

We know that C and A accept no upshot on each other.

We can too state the conditional independencies every bit follows:

• A is conditionally contained from C: P(A|B, C)
• C is conditionally independent from A: P(C|B, A)

Observe that the conditional dependence is stated in the presence of the conditional independence. That is, A is conditionally independent of C, or A is conditionally dependent upon B in the presence of C.

Nosotros might likewise country the provisional independence of A given C as the provisional dependence of A given B, as A is unaffected past C and tin be calculated from A given B alone.

• P(A|C, B) = P(A|B)

We tin can see that B is unaffected by A and C and has no parents; we can simply land the provisional independence of B from A and C as P(B, P(A|B), P(C|B)) or P(B).

We tin too write the joint probability of A and C given B or conditioned on B equally the product of two conditional probabilities; for example:

• P(A, C | B) = P(A|B) * P(C|B)

The model summarizes the joint probability of P(A, B, C), calculated as:

• P(A, B, C) = P(A|B) * P(C|B) * P(B)

Nosotros tin depict the graph every bit follows:

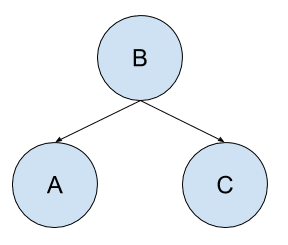
Example of a Simple Bayesian Network

Notice that the random variables are each assigned a node, and the conditional probabilities are stated as directed connections between the nodes. Likewise notice that it is not possible to navigate the graph in a cycle, e.1000. no loops are possible when navigating from node to node via the edges.

Also notice that the graph is useful even at this point where we don't know the probability distributions for the variables.

You might want to extend this example by using contrived probabilities for discrete events for each random variable and exercise some elementary inference for different scenarios.

Bayesian Networks in Python

Bayesian Networks can exist developed and used for inference in Python.

A pop library for this is called PyMC and provides a range of tools for Bayesian modeling, including graphical models like Bayesian Networks.

The most recent version of the library is called PyMC3, named for Python version 3, and was adult on top of the Theano mathematical ciphering library that offers fast automatic differentiation.

PyMC3 is a new open source probabilistic programming framework written in Python that uses Theano to compute gradients via automated differentiation as well as compile probabilistic programs on-the-fly to C for increased speed.

— Probabilistic programming in Python using PyMC3, 2016.

More by and large, the use of probabilistic graphical models in computer software used for inference is referred to "probabilistic programming".

This type of programming is chosen probabilistic programming, […] information technology is probabilistic in the sense that we create probability models using programming variables as the model'south components. Model components are first-class primitives within the PyMC framework.

— Bayesian Methods for Hackers: Probabilistic Programming and Bayesian Inference, 2015.

For an excellent primer on Bayesian methods generally with PyMC, see the free volume by Cameron Davidson-Pilon titled "Bayesian Methods for Hackers."

Further Reading

This section provides more resources on the topic if you are looking to go deeper.

Books

• Bayesian Reasoning and Machine Learning, 2012.
• Bayesian Methods for Hackers: Probabilistic Programming and Bayesian Inference, 2015.

Book Chapters

• Affiliate half-dozen: Bayesian Learning, Machine Learning, 1997.
• Chapter 8: Graphical Models, Pattern Recognition and Motorcar Learning, 2006.
• Chapter 10: Directed graphical models (Bayes nets), Car Learning: A Probabilistic Perspective, 2012.
• Chapter 14: Probabilistic Reasoning, Artificial Intelligence: A Mod Arroyo, 3rd edition, 2009.

Papers

• Probabilistic programming in Python using PyMC3, 2016.

Lawmaking

• PyMC3, Probabilistic Programming in Python.
• Variational Inference: Bayesian Neural Networks

Articles

• Graphical model, Wikipedia.
• Hidden Markov model, Wikipedia.
• Bayesian network, Wikipedia.
• Conditional independence, Wikipedia.
• Probabilistic Programming & Bayesian Methods for Hackers

Summary

In this mail, you discovered a gentle introduction to Bayesian Networks.

Specifically, y'all learned:

• Bayesian networks are a blazon of probabilistic graphical model comprised of nodes and directed edges.
• Bayesian network models capture both conditionally dependent and conditionally independent relationships betwixt random variables.
• Models tin exist prepared by experts or learned from information, then used for inference to estimate the probabilities for causal or subsequent events.

Do you have whatever questions?
Ask your questions in the comments below and I will do my best to answer.

Go a Handle on Probability for Auto Learning!

Develop Your Understanding of Probability

...with but a few lines of python code

Find how in my new Ebook:
Probability for Machine Learning

It provides self-report tutorials and end-to-end projects on:
Bayes Theorem, Bayesian Optimization, Distributions, Maximum Likelihood, Cross-Entropy, Calibrating Models
and much more than...

Finally Harness Dubiousness in Your Projects

Skip the Academics. Only Results.

See What's Inside

Source: https://machinelearningmastery.com/introduction-to-bayesian-belief-networks/

Posted by: charettebegather1962.blogspot.com

Share this post